手撕算法之排序算法

手撕算法之排序算法

排序算法应该是比较基本算法了，也是实践中比较容易用到的算法，同样也是面试中最容易问到的算法。所以对于基本的排序算法能达到提起则默写的程度是非常必要的。想想过往的面试经历中，排序算法也是经常问到并且需要手写的了。然而，扪心自问一下，除了面试前的刷题，貌似过段时间后再次提起，又是一头雾水，那么如何真正的掌握了排序算法，并且达到手撕的程度，这是一个问题？我想只有真正了解了算法的核心思想、加上不断地记忆才能真正掌握。

OK，为了达到以上两个问题，了解常见排序算法的核心思想，为了以后得不断重复记忆，特总结此文章。

排序算法我将从所谓的我认为简单易理解到困难排序解说，以及coding。

冒泡排序 （时间复杂度 最坏为 O(n^2), 最好为O(n)）

算法核心

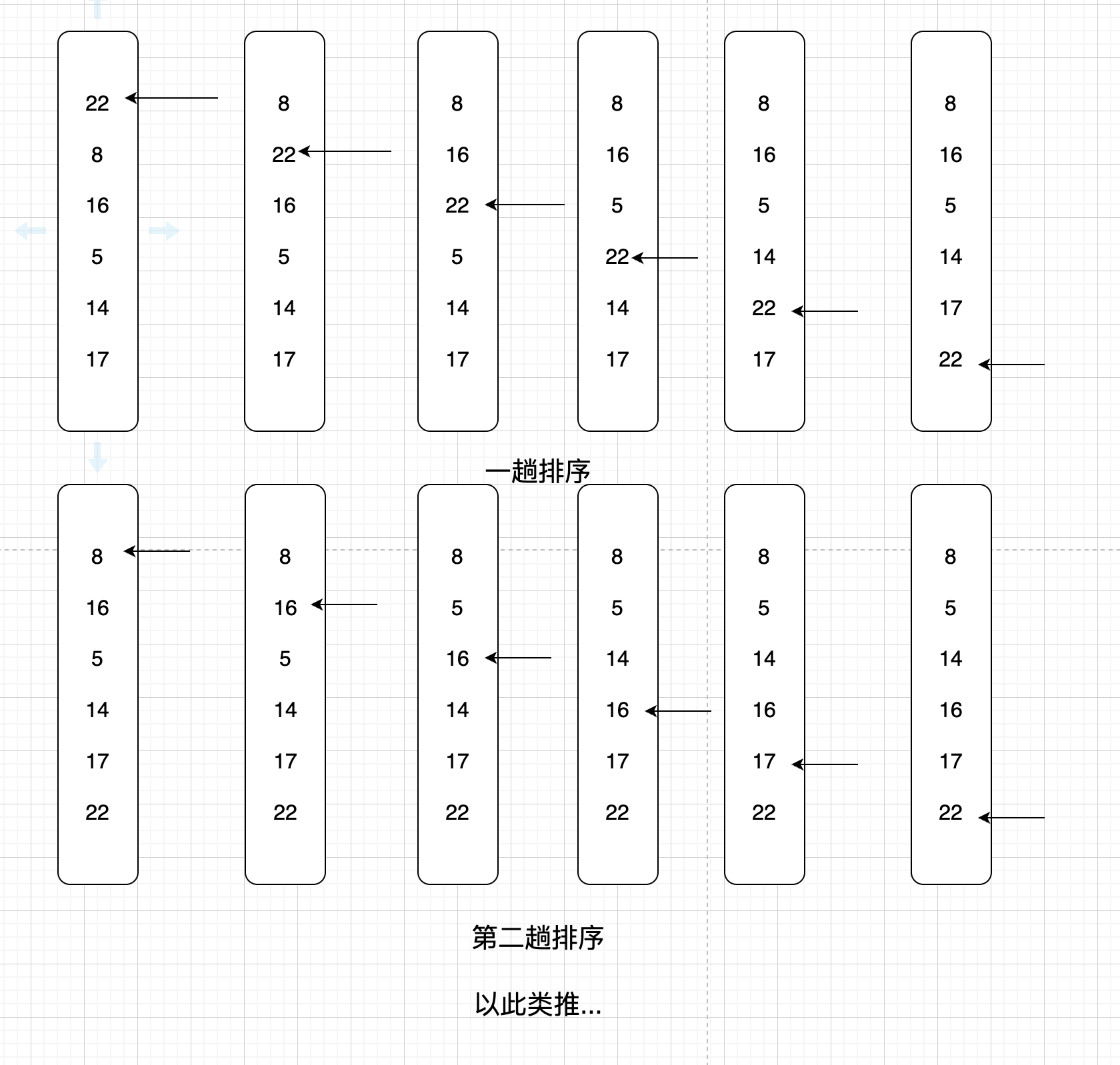
从头开始比较相邻两个元素，如果按照升序排，那么左边元素如果大于右边元素，则交换位置，否则不动，如果按照降序排，如果左边元素小于右边元素，则交换，否则不动。如此一遍为一轮。那么一轮下来我们能确定最大的元素即就是最有边的元素（升序的话），或者最左边的元素（降序的话）。如此类推，再次循环比较n-1个元素，按照以上规则再次比较，确定第二大元素….

图表示例

代码实现 （C/C++)

#include <iostream>

void bubbleSort(int arr[], int count) {
  if (n <= 1 || arr == NULL) {
    return;
  }
  	for (int i = 0; i < count; i++) {
      for (int j = 0; j < count - 1 - i; j++) {
        if (arr[j] > arr[j+1]) {
          int temp = arr[j];
          arr[j] = arr[j+1];
          arr[j+1] = temp;
        }
      }
    }
}

算法概要

核心思想则是，相邻元素比较大小，一趟能确定一个此比较中最大的数字。冒泡排序是稳定算法（即相同元素经过排序后顺序不会改变）。

选择排序 （时间复杂度 最好 最坏都为O(n^2)）

算法核心

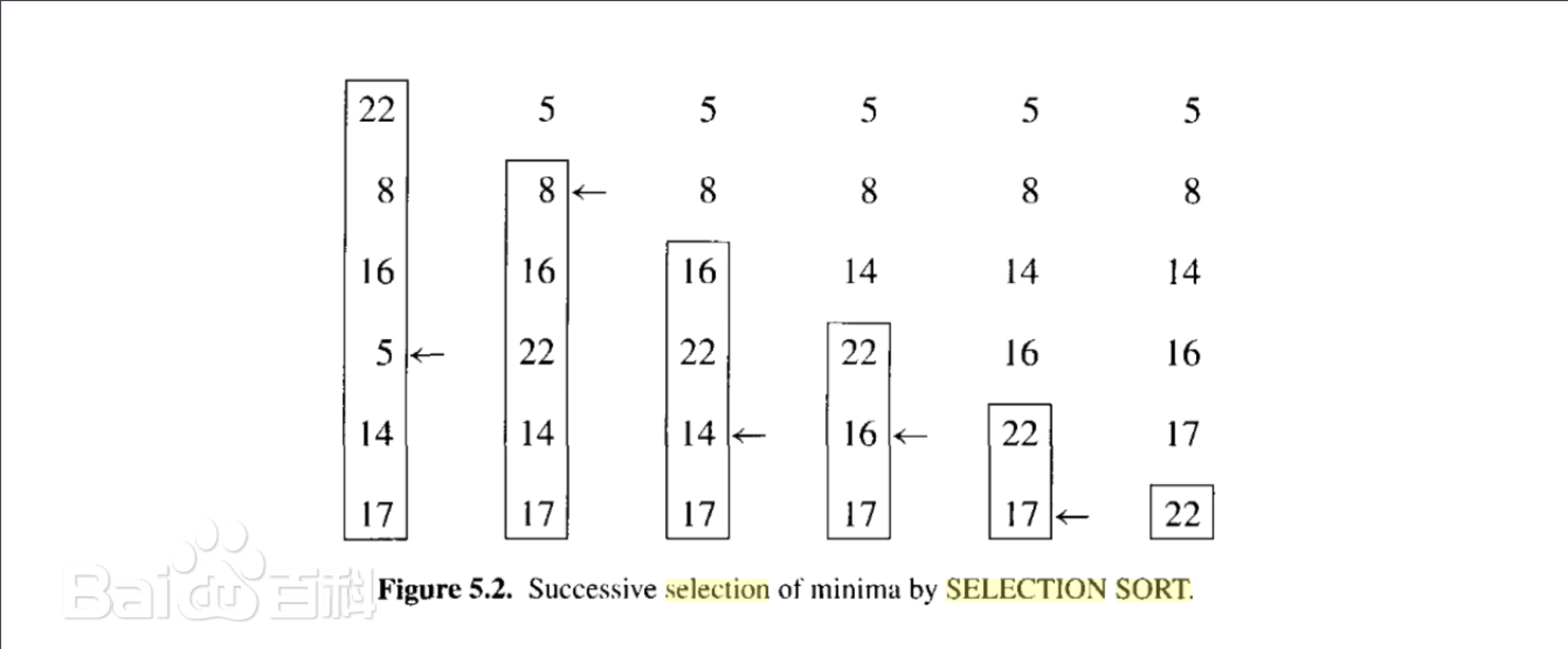
从未排序的组数中找出最小（升序）或者最大（降序）的元素放到数组第一位。其实感觉起来和冒泡很像，冒泡排序是比较相邻的两个元素进行比较，然后进行交换或者不交换。选择呢则是遍历整个未排序数组找出最小或者最大的元素，与未排序的数组第一个元素交换。

图标示例：

代码实现（C/C++）

void selectSort(int arr[], int n) {
  if (n <= 1 || arr == NULL) {
    return;
  }
  for (int i = 0; i < n; i++) {
    int minIndex = i;
    for (int j = i + 1; j < n; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }
    int temp = arr[i];
    arr[i] = arr[minIndex];
    arr[j] = temp;
  }
}

算法概要

从未排序的数组中找出最小或者最大的元素，放到未排序数组第一个元素。此算法也是稳定算法。

插入排序（最好O(n), 最坏O(n^2), 平均O(n^2)）

算法核心

将数组分为有序和无序数组，默认当前位置之前是有序数组，之后是无序数组。从有序数组中从后往前找到合适位置插入无序元素。

举个很现实的例子：比如我们打扑克牌。手里的牌已经是排好的，我们抓一张牌，找到合适的位置插入。

图表示例

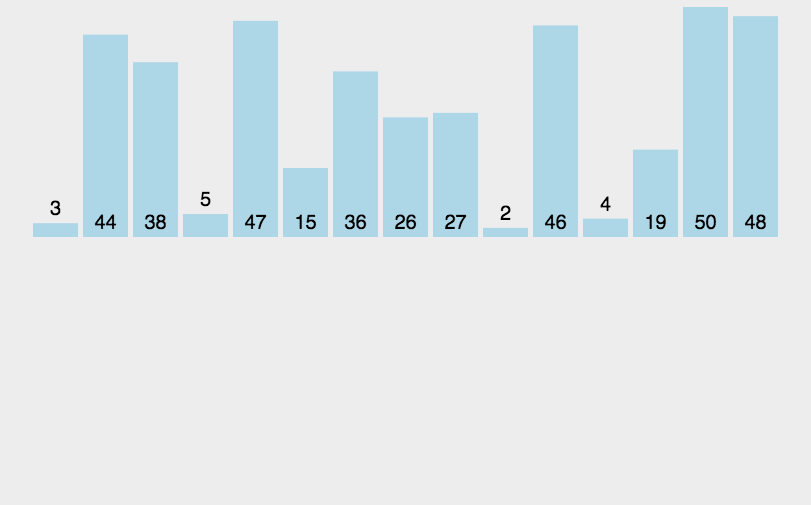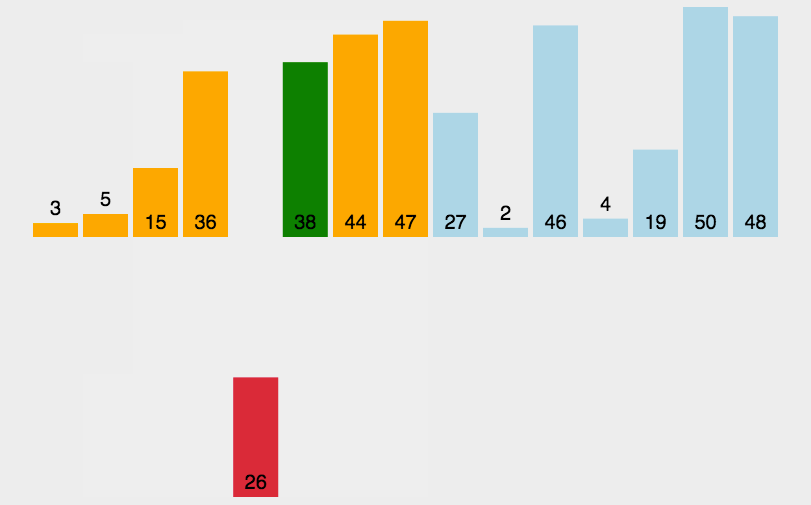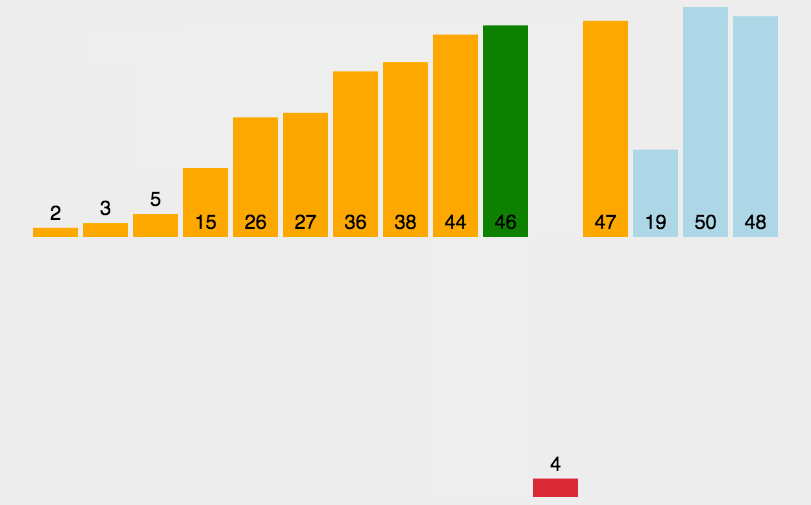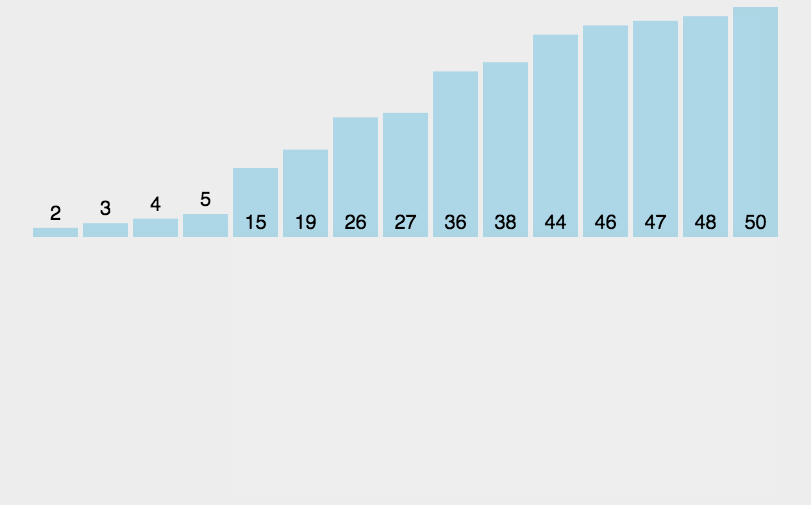
代码实现

void insertSort(int arr[], int n) {
  if (n <= 1 || arr == NULL) {
    return;
  }
  
  for (int i = 1; i < n; i++) {
    int temp = arr[i];
    int j = i - 1;
    while (j >= 0 && arr[j] > temp) {
      arr[j+1] = arr[j];
      j--;
    }
    arr[j+1] = temp;
  }
}

算法概要

插入算法，核心就是从有序数组中从后往前找到无序数组元素合适的位置插入，但是具体语言不通，插入方法不通，有些高级语言可以直接利用语言提供的语法直接插入如OC、swift。但是c或者c++，则需要先移动后替换（即比较有序元素中比无序元素大元素往后移一位，最后则将正确位置替换成排序元素）。但是核心则都是一致的。

归并排序（O(nlogn)）

算法核心

归并算法采用分治思想，将一个大问题分解为若干个小问题，将每个小问题求解后合并得到大问题的解。

具体步骤为：

1. 将待排序序列对半分开，然后继续二分，最终我们得到一个只有1个元素的子数组
2. 将这些最小子数组两两合并，我们每次合并的结果必须是有序的
3. 将子问题的解，也就是稍大颗粒度的子数组的解合并，最后得到有序的数组

图表示例

代码实现

void merge_recursive(int arr[], int res[], int start, int end) {
  // 如果start >= end 说明只有1个元素或者没有元素
  if (start >= end) {
    return
  }
  
  // 获取区间长度
  int len = end -start;
  // 获取中间下标
  int mid = (len >> 1) + start;
  // 二分之后的第一组开始下标
  int start1 = start;
  // 二分之后的第一组结束下标
  int end1 = mid;
  // 二分之后的第二组开始下标
  int start2 = mid + 1;
  // 二分之后的第二组结束下标
  int end2 = end;
  
  // 继续递归第一组
  merge_recursive(arr, res, start1, end1);
  // 继续递归第二组
  merge_recursive(arr, res, start2, end2);
  
  int p1 = start;
  // 如果两个序列都正常，则比较对应下标的值，值小的插入res数组中
  while (start1 <= end1 && start2 <= end2) {
			res[p1++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
  }
  // 如果只有左边正常，则插入res数组中
  while (start1 <= end1) {
    res[p++] = arr[start1++];
  }
  // 如果只有右边正常，则插入res数组中
  while(start2 <= end2) {
    res[p++] = arr[start2++];
  }
  // 将res对应的下边替换对应arr下标的值
  for (p1 = start; p1 <= end; p1++) {
    arr[p1] = res[p1];
  }
}

void merge_sort(int arr[], int n) {
  int res[n];
  merge_recursive(arr, res, 0, n - 1);
}

算法概要

归并算法的核心就是分治思想，分治思想的核心，就大问题拆解成小问题求解，然后将小问题的解合并成大问题的解。分治思想其实比较合适的也就是用递归思想实现。

快速排序（平均O(nlogn), 最坏 O(n^2)）

算法核心

快速排序其实也是分治思想，将大问题拆分为小问题求解，小问题的解合并成为大问题的解。

其核心为，找一个基准值，将序列分为两个序列，其中左边小于等于基准值，右边都大于等于基准值。然后继续重复刚才的步骤进行，知道拆分序列为空或者只有一个元素。

图表示例

代码实现

void partition(int arr[], int low, int high) {
  // 第一个元素作为基准值
  int pivot = arr[low];
  
  while(low < high) {
    // 从基准右边由高向低找直到找到一个比基准值小的元素
    while (low < high && arr[high] >= pivot) {
      --high;
    }
    // 将这个元素和low 下标交换，即把比基准小的元素放到左边
    arr[low] = arr[high];
    
    // 从基准左边由低向高找直到找到一个比基准值大的元素
    while (low < high && arr[low] <= pivot) {
      ++low;
    }
    // 将这个元素和high 下标交换，即把比基准小的元素放到右边边
    arr[high] = arr[low];
  }
  // 将基准值插入到对应位置
  arr[low] = pivot;
  return low;
}

void quick_sort_recursive(int arr[], int low, int high) {
  if (low < high) {
    int pivot =  partition(arr, low, high);
    quick_sort_recursive(arr, low, pivot - 1);
    quick_sort_recursive(arr, pivot + 1, high);
  }
}
void quick_sort(int arr[], int n) {
  if (n < 2 || arr == NULL) {
    return
  }
  quick_sort_recursive(arr, 0, n - 1);
}

算法概要

快排的算法概要就是1.分治思想 2. 基准值（左边元素都比基准值小，右边元素都比基准值大）。

堆排序（平均复杂度为O(nlogn))

算法核心

概念

• 二叉树、满二叉树、完全二叉树

  度：二叉树的度，标识每个节点孩子数

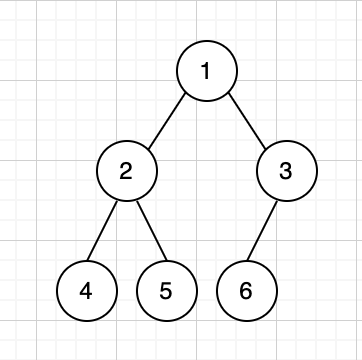
  二叉树：一棵树只有两个分支，即只有左子树和右子树的情况数，被称之为二叉树， 如下图

  

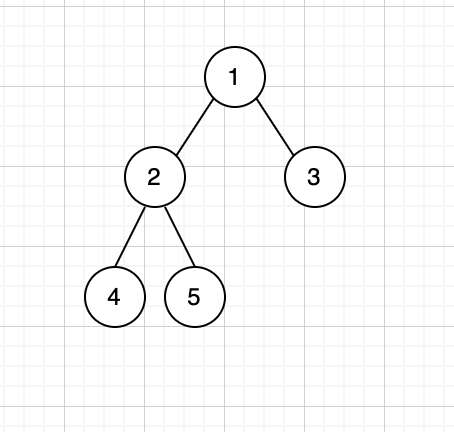
  满二叉树：如果一个二叉树的度为2，即每个节点都有两个孩子，则称之为满二叉树

  

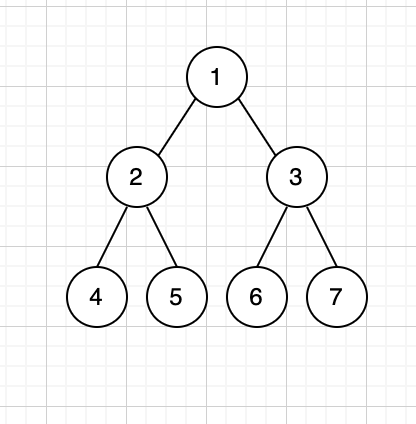
  完全二叉树：完全二叉树是在满二叉树的基础上来的，它要求，去掉最后一层叶子节点后，必须为满二叉树，且最后一层叶子节点必须从左到右（也就是说不能只有右叶子，没有左叶子）

  

• 堆的概念

  了解以上数的概念后，我们来了解堆的概念。

  堆我们可以理解为一个近似完全二叉树，且子节点的值必须小于（或者大于）其父节点的值。

  堆分为大顶堆和小顶堆，大顶堆则为：每个节点的值都大于或者等于其子节点的值，通常用作升序排序；小顶堆则为：每个节点的值都小于等于其子节点的值，可用作降序排序。为何大顶堆可用作升序，小顶堆可用作降序？当我们理清堆排序的特点和流程之后，就会明白。

  得知某个节点下标x，可知：

  左子树下标为：x « 1 + 1

  右子树下标为：x « 1 + 2

  得知某个子节点下标为x，可知：

  父节点下标为：(x - 1)  » 1

• 堆排序

  我们利用堆的数据结构，以升序排序来说，可以构建大顶堆。堆排建堆是关键。以下我们以建大顶堆为例（小顶堆反过来一样）

  建堆过程：

  1. 从最后一个叶子节点的父节点开始比较，取其子节点中最大的比较，如果比父节点大则交换，否则不动；
  2. 交换完成后，继续子节点进行向下比较，同样进行1中的比较
  3. 直到所有节点都处理完成，则这个时候就形成了一个大顶堆。根节点的值是最大的。

  排序过程：

  1. 首先进行一次建堆过程，此时得出最大值为a[0]
  2. 从i=n-1开始遍历序列，每次交换a[0]与a[i]的位置，然后再次进行建大顶堆从区间0-(i-1)。
  3. 以此类推，直到遍历完成，则升序序列也排好了。

图表示例

初始化堆

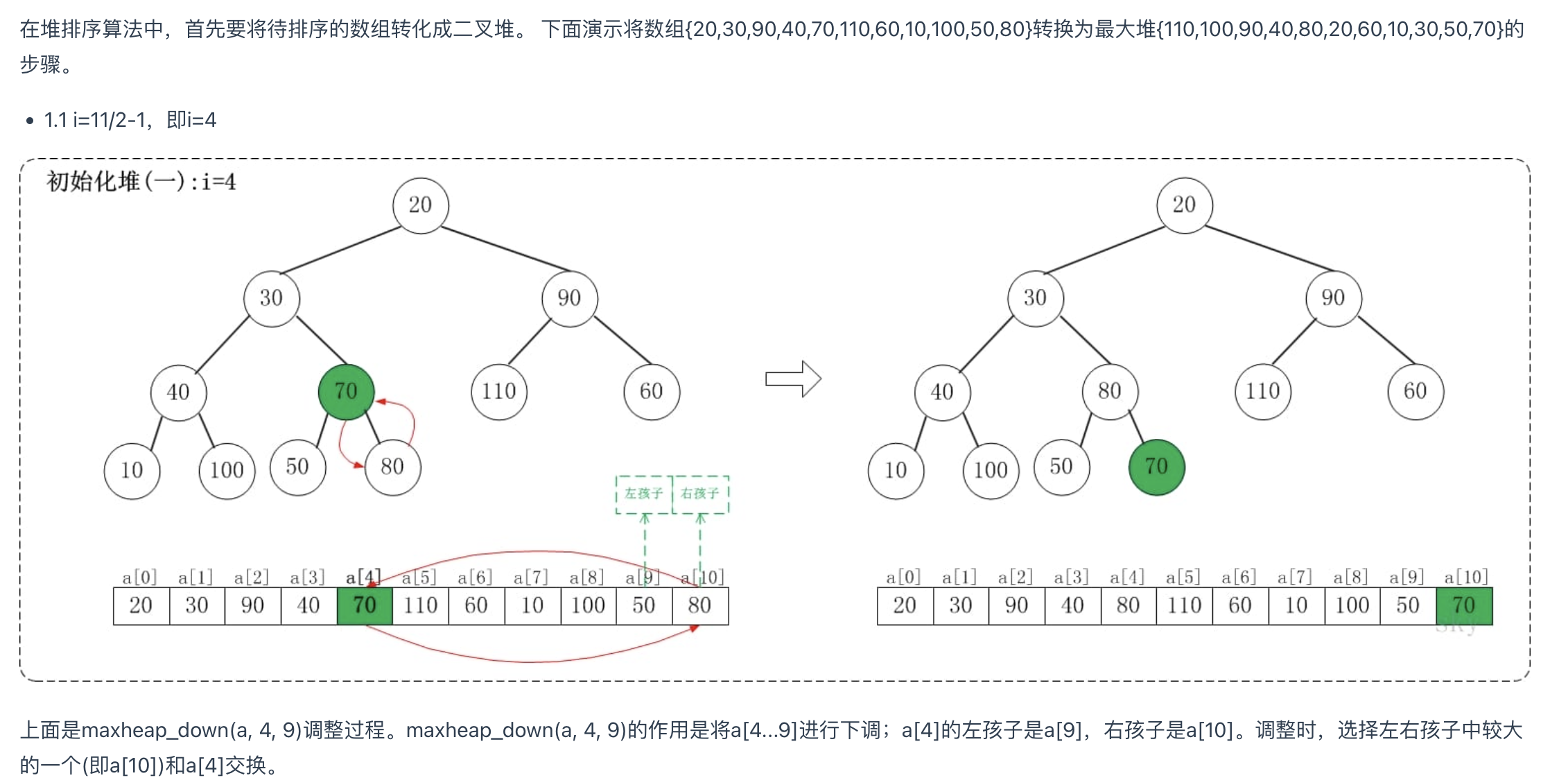
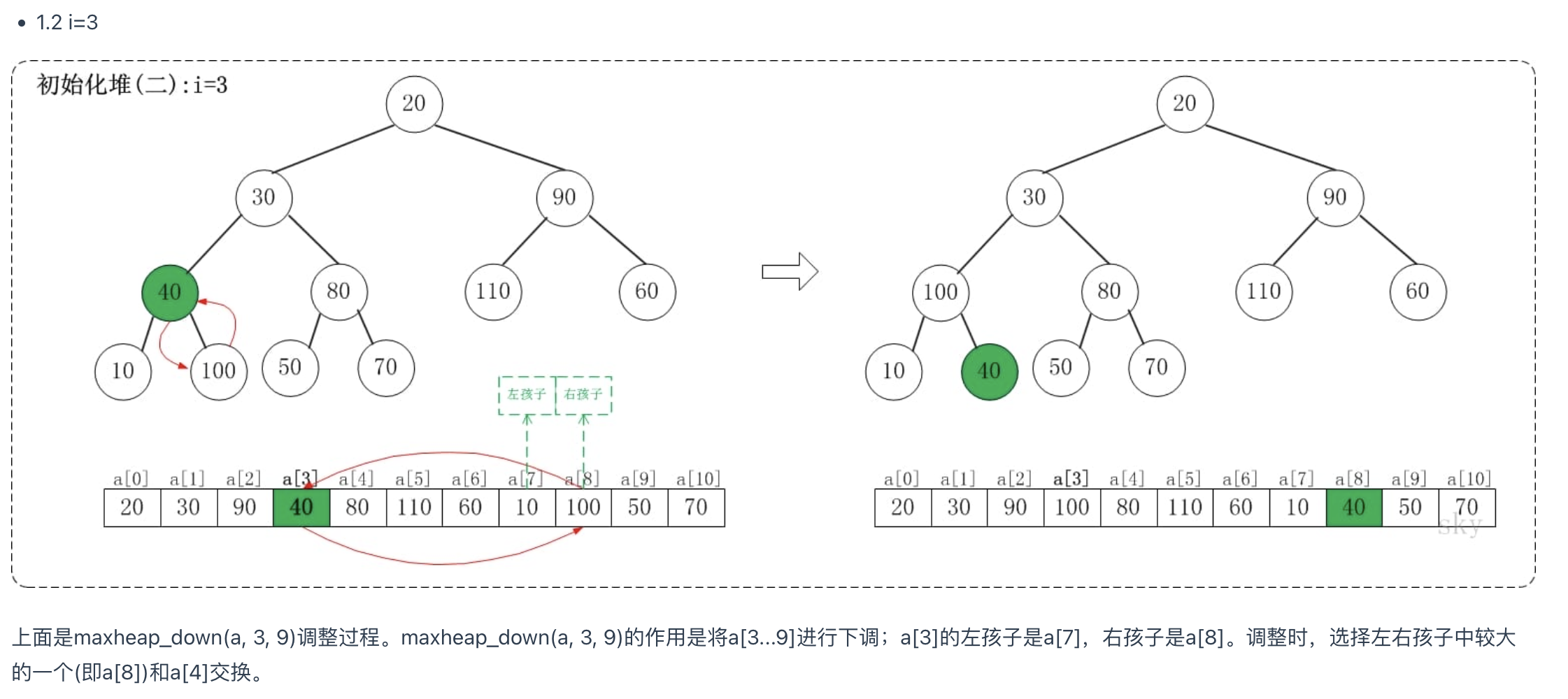
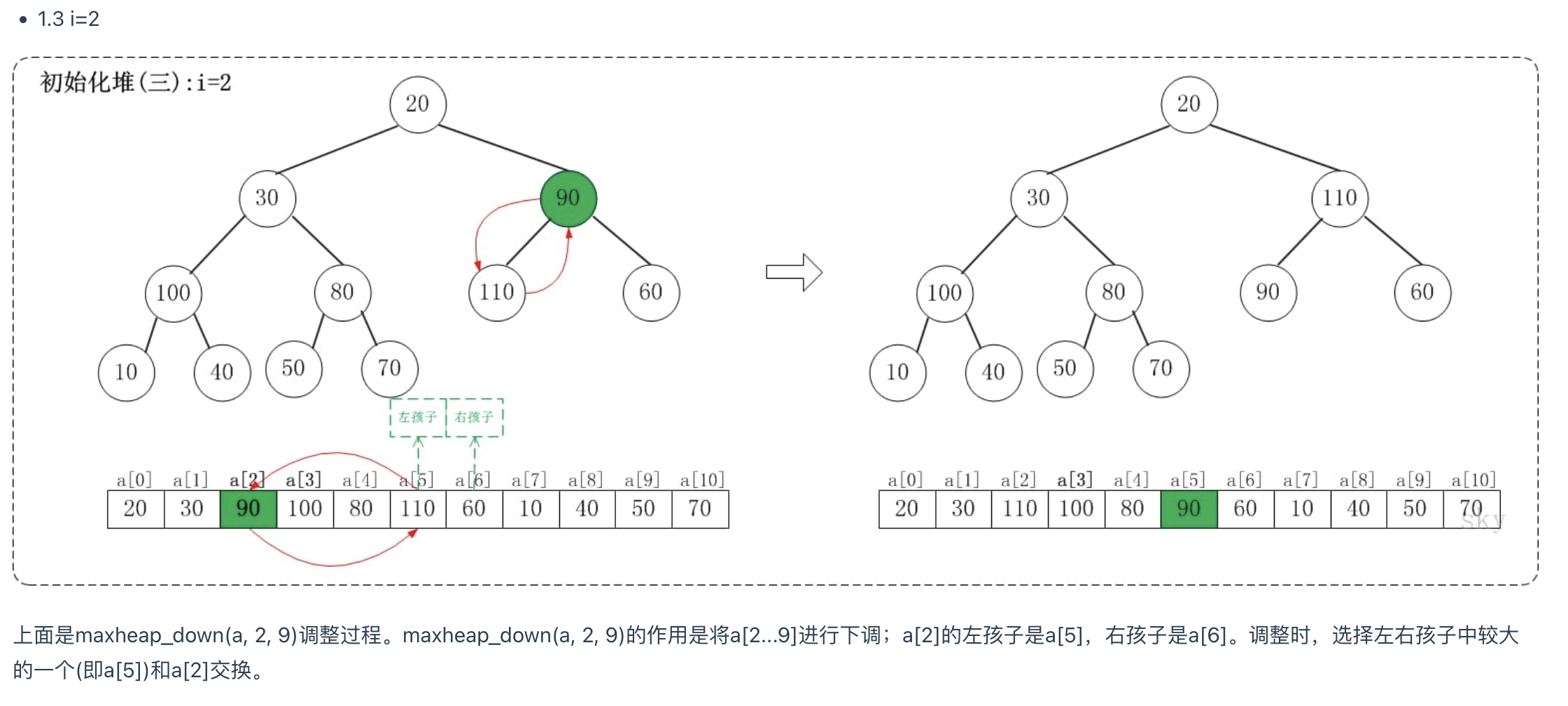
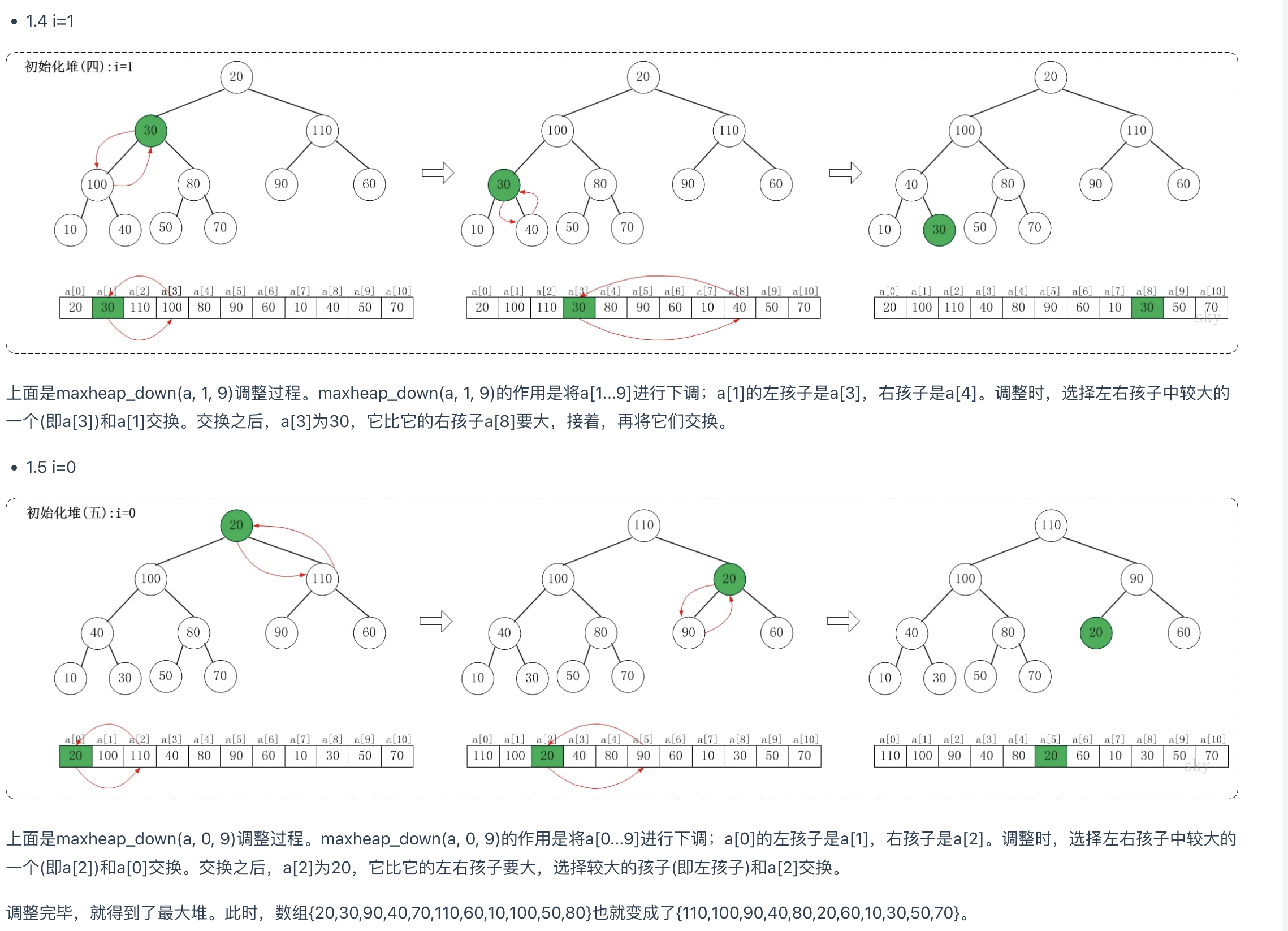
堆排序

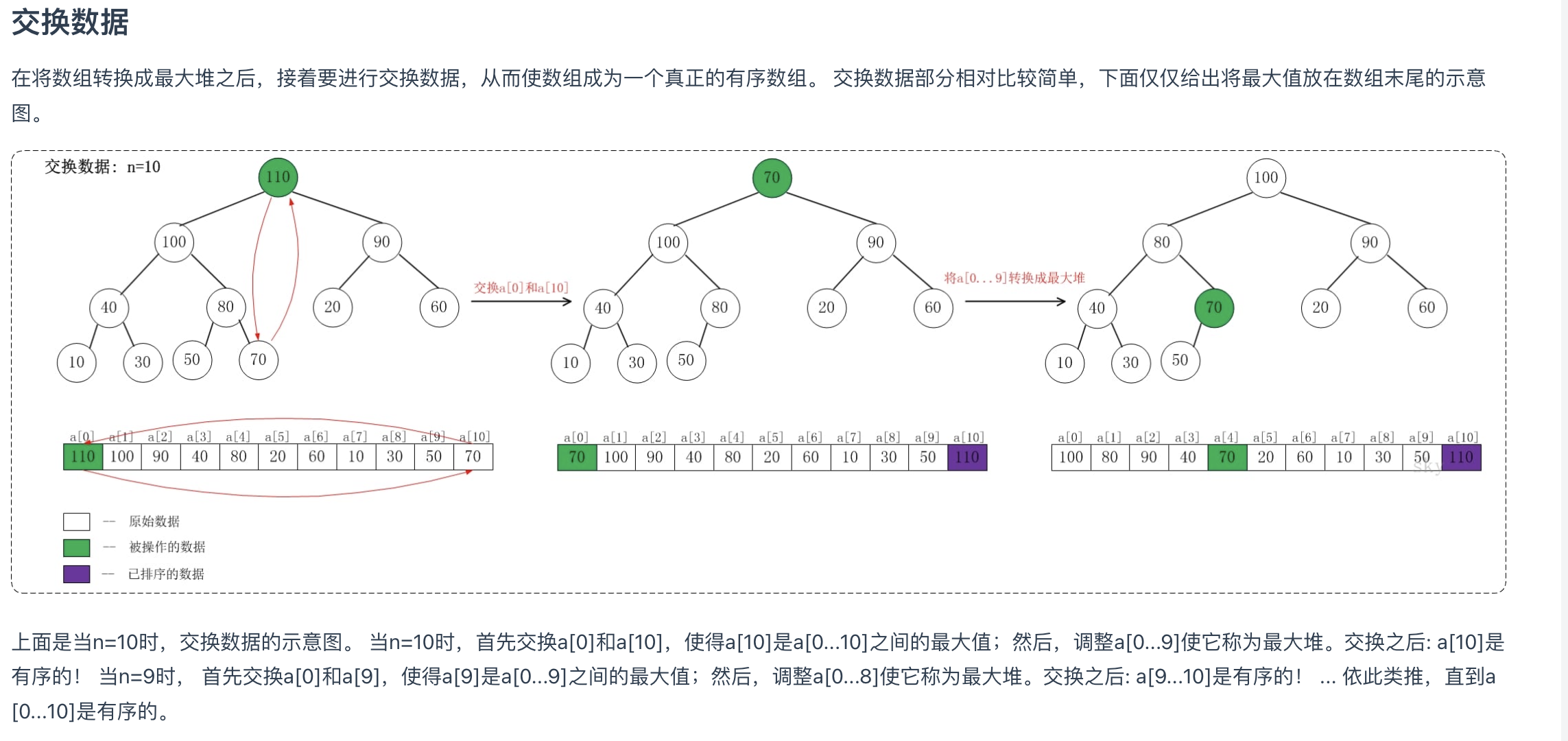
代码实现

void swap(int *a, int *b) {
  int temp = *a;
  *a = *b;
  *b = temp;
}

// 创建大顶堆
void build _max_heap(int arr[], int start, int end) {
  int parent = start;
  int child = (parent << 1) + 1;
  
  while (child <= end) {
    if (child + 1 <= end && arr[child] < arr[child + 1]) {
      child++;
    }
    if (arr[parent] > arr[child]) {
      return;
    } else {
      swap(&arr[parent], &arr[child]);
      parent = child;
      child = (parent << 1) + 1;
    }
  }
}

void heap_sort(int arr[], int n) {
  if (arr == NULL || n < 2) {
    return;
  }
  for (int i = (n >> 1) - 1; i >= 0; i--) {
    build_max_heap(arr, i, n - 1);
  }
  
  for (int i = n - 1; i >= 0; i--) {
    swap(&arr[i], &arr[0]);
    build_max_heap(arr, 0, i - 1);
  }
}

算法概要

堆排序重要概念则是，1.如何知道父节点下标获取子节点下标，以及子节点下标获取父节点下标 2. 建立大顶堆、小顶堆的步骤过程 3、排序值交换。掌握这三个则掌握了堆排序

总结

算法需要了解数据结构，掌握其内在理论，明白其算法核心，才能掌握。当然我非聪明之人，真正的掌握还需要长期反复的复习，才能达到真正的掌握。